Loading... > ##### P.S. > > **今天讲数据结构,大概包括了二叉堆,二叉搜索树,线段树,树状数组,并查集,st表,RMQ,LCA。** 二叉堆 --- * 基本功能 1. O(log n)插入元素 2. O(1)查最大(最小)元素 3. O(log n)删除最大(最小)元素 4. O(log n)删除任意元素 * 基本结构 * 最为常用的堆结构就是完全二叉堆。 * 在逻辑形式上,结构必须等同于完全二叉树,同时,堆顶以外的每个节点都不大于(小于)其父亲,即堆有序。 * 如果堆顶最大,称为最大二叉堆(大根堆),反之称为最小二叉堆(小根堆)。 * 因为完全二叉堆等同于完全二叉树的结构,故高度相当。为O(log n). * 一般为了实现方便,根节点编号为1,节点n左节点为2n,右节点为2n+1. ##### 查询操作 * 最大(最小),直接返回堆顶即可。 ##### 插入操作 * 首先把新元素插入向量末尾,为了维持堆的有序性,逐层检查是否有序并调整,过程通常称为上滤。 ##### 建堆 * O(n log n)插入每个元素即可。 * O(n)? * 先随机放入一个完全二叉树。 * 从倒数第二个深度开始检索,使堆有序。 ##### 删除最大(最小)元素 * 首先将堆顶元素与堆尾元素交换。 * 删除堆尾元素。 * 一步一步将这个换上去的元素下移。 * 直到堆有序。 ##### 删除任意元素 \- 新建一个堆,将删除的元素放入新堆里。即可实现删除。 ---------------------------- 二叉搜索树 ----- * 基本功能 * 排序 * 查询元素大小排名 * 插入元素 * 二叉平衡树的基础 * 结构 * 若左子树不为空,则左子树上所有节点小于根节点。 * 若右子树不为空,则右子树上所有节点大于根节点。 * 左右子树也分别称二叉排序树。 * 排序 * 中序遍历 * 查询元素大小排次 * 从根开始向左、右是唯一的,如果向右,那么将左边的节点数加起来,反之不加。 * 插入 * 与查询方法类似。 \- 查询到节点后向上更新其他节点。 ------------------ 线段树 --- * 基本功能 * 建树 * 单点查询 * 单点修改 * 区间查询 * 区间修改 * 结构 * 是一棵二叉搜索树,每个节点代表一个区间。 * 每个节点需要维护 * 区间左右端点 * 区间要维护的信息 * 基本思想:二分 * 特殊性质 * 左子节点区间为\[l,mid\],右为\[mid+1,r\]. * 对于一个节点k,左子节点为2k,右子节点为2k+1. * 建树 * 对于二分的每一个节点,确定其代表的区间。 * 如果为叶子结点,存需要维护的信息。 * 对于非叶子结点,将两个子节点状态合并。 * 单点查询 * 在左右节点搜索是确定的,由节点的mid决定,如果要查询的点大于mid,则在右子树搜索,反之在左子树搜索。代码如下: `cpp #include<bits/stdc++.h> using namespace std; #define LL long long const int MAXN = 100000; struct tree{ int l,r,s; }mi[4*MAXN+20]; void build(int k,int l,int r){ mi[k].l=l; mi[k].r=r; if(l==r){ mi[k].s=r; return; } int mid=(l+r)/2; build(2*k,l,mid); build(2*k+1,mid+1,r); mi[k].s=mi[k*2].s+mi[k*2+1].s; } int search(int k,int n){ if(mi[k].l==mi[k].r&&mi[k].r==n){ return k; } int mid=(mi[k].l+mi[k].r)/2; if(n<=mid) return search(k*2,n); else return search(k*2+1,n); } int main(){ build(1,1,6); cout<<search(1,5); return 0; }` * 单点修改 * 先执行单点搜索,然后执行修改操作,再向上更新状态。 * 代码如下 ```cpp int insert(int k,int n,int v){ int now=search(k,n); mi[now].s+=v; while(now!=1){ now/=2; mi[now].s=mi[2*now].s+mi[2*now+1].s; } }``` * 区间查询 * 令\[l,r\]为当前节点代表的区间,mid代表区间中点,\[x,y\]代表要查询的区间。 * 若\[l,r\]=\[x,y\]直接返回即可。 * 如果$y\\leq mid$,\[l,r\]->\[l,mid\],\[x,y\]不变,递归查询。 * 如果$x > mid$,\[l,r\]->\[mid+1,r\],\[x,y\]不变,递归查询。 * 否则,\[x,y\]跨过了mid的两端,将其分成了两个子问题,$\[l,mid\]$中查$\[x,mid\]$.$\[mid+1,r\]$中查$\[mid+1,y\]$. * 代码如下: `cpp int query_sum(int k,int x,int y){ if(y<mi[k].l||x>mi[k].r) return 0; if(x==mi[k].l&&mi[k].r==y) return mi[k].s; int mid=(mi[k].l+mi[k].r)/2; return query_sum(k*2,x,mid)+query_sum(k*2+1,mid+1,y); }` * 区间修改 * 关键:懒标记 * 经过节点的集合与区间查询相同 * 更新这些区间的答案并打上一个标记,来表示这个区间中的数要进行哪些修改。 * 只有当查询或者修改经过一个节点时,才将其节点上的懒标记放到两个孩子节点,下放的同时修改两个孩子节点的答案。 #### 模板(无区间修改) /*求和线段树*/ #include<bits/stdc++.h> using namespace std; #define LL long long #define inf 2147483647 const int MAXN = 100000; struct tree{ int l,r,s; }mi[4*MAXN+20]; void build(int k,int l,int r){ mi[k].l=l; mi[k].r=r; if(l==r){ mi[k].s=r; return; } int mid=(l+r)/2; build(2*k,l,mid); build(2*k+1,mid+1,r); mi[k].s=mi[k*2].s+mi[k*2+1].s; } int search(int k,int n){ if(mi[k].l==mi[k].r&&mi[k].r==n){ return k; } int mid=(mi[k].l+mi[k].r)/2; if(n<=mid) return search(k*2,n); else return search(k*2+1,n); } int query_sum(int k,int x,int y){ if(y<mi[k].l||x>mi[k].r) return 0; if(x==mi[k].l&&mi[k].r==y) return mi[k].s; int mid=(mi[k].l+mi[k].r)/2; return query_sum(k*2,x,mid)+query_sum(k*2+1,mid+1,y); } int insert(int k,int n,int v){ int now=search(k,n); mi[now].s+=v; while(now!=1){ now/=2; mi[now].s=mi[2*now].s+mi[2*now+1].s; } } int main(){ int n,m,x,v; cin>>n>>m>>x>>v; build(1,n,m); cout<<query_sum(1,x,v); return 0; } * * * 树状数组 ---- * 基本功能 * 单点修改,前缀信息查询。 * 区间修改可减信息(前缀和),单点查询。 * lowbit函数 * 含义:一个数,二进制表示中的最后一个1。 * 计算机中负数的表示? * 怎么求lowbit呢? * $x and (-x)$ * 结构 * 我们定义c\[i\]为区间$\[i-lowbit(i)+1,i\]$。 * 怎么直观的看一看呢? 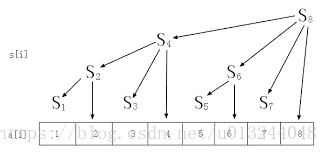 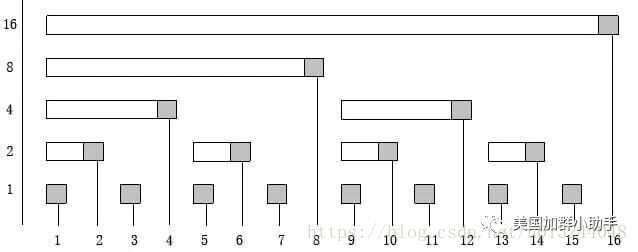 * $S\_n=S\_{(n-lowbit(n))}+C_n$ * 查询代码 int sum(int x){ int ans=0; for(;x;x-=lowbit(x)) ans+=c[x]; return ans; } * 修改代码 void update(int x,int v){ for(;x<=n;x+=lowbit(x)) c[x]+=v; } * 代码示例: #include<bits/stdc++.h> using namespace std; const int maxn=100010; int a[maxn],c[maxn]; int n; int lowbit(int x){ return x&(-x); } int sum(int x){ int ans=0; for(;x;x-=lowbit(x)) ans+=c[x]; return ans; } void update(int x,int v){ for(;x<=n;x+=lowbit(x)) c[x]+=v; } int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; update(i,a[i]); } cout<<sum(n); return 0; } * 区间修改,单点查询 * 且以修改为加法,查询为求和为例。 \- 对于将$\[l,r\]$加$x$的操作,可以将点$l$加$x$,将点$r+1$减$x$,这时候求点$n$的前缀和就能得到点$n$真实的值。 ------------------------------------------------------------------------ 并查集 --- * 基本功能 * 合并两个集合 * 查询某一个元素属于哪个集合 * 结构 * 并查集S由若干子集合$S_i$构成,并查集的逻辑结构是一个森林。 * $S_i$表示森林中的一颗子树。 * 一般以子树的根作为该子树的代表。 * 而对于并查集的存储结构,可用一维数组来实现。 * 查询某个元素属于哪个集合 * 通常而言都是以根作为这个集合的代表元。 * 因此只需要不断向父亲节点走,直到走到根为止返回即可。 * 合并集合  * 路径压缩优化  * 示例代码 \`\`\`cpp #include<bits/stdc++.h> using namespace std; int fa\[200010\]; int n; int find(int x) { if(fa\[x\] == 0) return x; return fa\[x\] = find(fa\[x\]); } void add(int x,int y){ int xx=find(x),yy=find(y); fa\[yy\]=xx; } int main(){ cin>>n; int x,y,m,z; for(int i=0;i<n;i++){ cin>>x>>y; add(x,y); } cin>>m>>z; cout<<find(m)<<" "<<find(z); return 0; }</li> </ul> <h2> \`\`\` RMQ问题 ----- * R——Range * M——Minimum/Maximum * Q——Query * 即区间最值问题 ### 例题  \- 方法1:使用线段树 - 方法2:st表 ### ST表 * 基本功能 * $O(nlogn)$预处理,$O(1)$查询区间最值。 * 结构 * $f\[i\]\[j\]$表示区间$\[i,i+2^j-1\]$的信息。 * 整个$f$数组就是ST表。 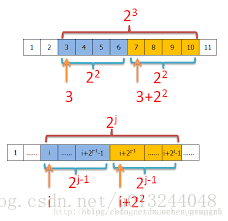 * 建表 * $f\[i\]\[0\]$就是单点i的信息 * 当$j>0$时,$f\[i\]\[j\]$为$f\[i\]\[j-1\],f\[i+2^{j-1}-1\]\[j-1\]$两个区间信息的并集。 * 查询 * 比方说我们要查询区间$\[x,y\]$的信息。 * 令t为最大的正整数使得$2^t\\leq y-x+1$ * 那么答案就是$\[x,x+2^t-1\]\\cup\[y-2^t+1,y\]$ * 代码如下: #include<bits/stdc++.h> #define maxn 111100 #define logN 25 //因为cmath中的log函数效率差,不如直接设定一个永远到不了的值 using namespace std; int f[maxn][logN],a[maxn],n,m; void pre_st(){ //制表 for(int i=1;i<=n;i++) f[i][0]=a[i]; //因为第二个框框中存的j是用来计算 i+2^j-1(既该f保存的值) //服务于动态规划的结果 for(int j=1;j<=logN;j++){ for(int i=1;i+(1<<j)-1<=n;i++) f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]); //注释1 (1<<j)是计算出 2^j 把一一直右移即可得到 //注释2 使用刚才得到的动态规划方程 } } int main(){ cin >> n;cin >> m; for(int i=1;i<=n;i++) scanf("%d",&a[i]); pre_st(); //制表 int x,y; for(int i=1;i<=m;i++){ cin >> x >> y; int s=log(y-x+1)/log(2); //计算出这一段距离之中最大的2的倍数,以查表 cout << max(f[x][s],f[y-(1<<s)+1][s]) << endl;; //合并左右不分的解 } return 0; } * * * 查询树上两点的最近公共祖先(LCA) ------------------ * L——Lowest * C——Common * A——Ancestor * 即最近公共祖先 ### 欧拉序 * 一种特殊的dfs序,每到达一个点就加入序列。 * 记录每个点第一次出现的时间$S\[u\]$,欧拉序中第i个点为$Q\[i\]$。 * $LCA(x,y)$是$Q\[S\[x\]...S\[y\]\]$中层数最低的点。 * 区间最值? * ST表! Last modification:March 14, 2020 © Allow specification reprint Like 如果觉得我的文章对你有用,请随意赞赏